The probability of entering checkers from the bar

Last updated on March 9, 2024

Beginners guides. How to play backgammon.

This Deluxe Backgammon post is another in our series for absolute beginners. In this post, we are going to examine the maths behind re-entering checkers from the bar. Understanding these numbers is important as they affect the tactics you apply to each turn. In particular, it determines how aggressively you can play and where you can leave blots or builders.

Note: the percentages in this post are all rounded up to whole numbers.

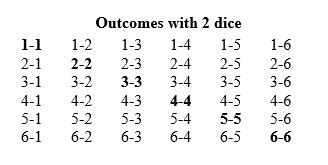
The possible outcomes of a roll of the dice

Each die has 6 sides, each numbered from 1 to 6. Opposing sides of the dice will always add up to a total of seven. When a die is rolled one of those six numbers will be face up and it provides the number to be played. Therefore, with 2 dice the total number of possible outcomes that can occur when thrown is 6 x 6, or 36 combinations. The possible rolls are shown in the table below:

From the table, the following conclusions can be concluded:

1. For any one double, for example, 3-3, there is only one combination that gives the required result. Therefore, the chances of rolling a specific double are 1 in 36 or 3%.
2. For any unmatching pair of numbers, for example, 5 and 6), there are always two combinations which will give the result required (5-6 and 6-5). Therefore, the chances of rolling any two particular different numbers together are 2 in 36 or 6%.
3. For any single number, for example, 1, there are eleven outcomes which include that number (6-1, 5-1, 4-1, 3-1, 2-1, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6). Therefore, the chances of a roll that includes any one particular number are 11 in 36 or 31%.

We can factor in these conclusions when we are considering our tactical and strategic planning, particularly in terms of risk. These conclusions can help us determine how likely we will be able to re-enter from the bar when hit. If we take the first conclusion as an example. Imagine, you are considering leaving multiple blots on the board as builders and these checkers are within range of your opponent’s checkers. If those two blots get hit and your opponent has 5 secure points in their home board, you have only a 3% chance of escaping those checkers in a single roll. However, if only one of those blots gets hit, based on conclusion three, there is a 31% chance of escaping on a single roll.

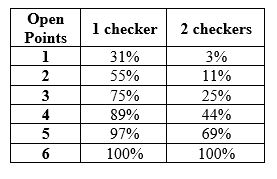
The probability of getting one or two checkers off the bar with X open points.

These numbers are important when considering your strategy for upcoming moves. The stronger your opponent’s home board (the fewer open points), the more defensive your tactics and strategy will need to be. This is because the fewer open points there are, the harder it is to return from the bar.

Opening moves

At the start of the game, your opponent only has one secure point in their home board, which is the 6-point, stacked with 5 checkers. Therefore, you have 5 open points, which gives you a 97% chance of returning to the board if hit. This means you can only fail to re-enter if you roll a double 6. As the game progresses you would expect your opponent to strengthen their home board. This results in a reduced chance of re-entry. This is why you should consider splitting your back checkers early, while the board is still open. Splitting early gives you the chance to secure an advanced anchor, which provides a significant tactical advantage.

It is also worth considering being aggressive early, elsewhere on the board. Slotting and placing builders early in the game is a wise move because if you are hit, the chances of re-entry are still high. Placing builders early in the game allows you to target key points, such as the bar or 5-points, on subsequent throws. If the risk pays off it will confer a significant advantage. If it doesn’t pay off and you are hit, the board is still reasonably open for re-entry.

Middle game

As the game progresses and your opponent improves the structure of their home board by securing more points, it becomes more dangerous to be hit. They could potentially close their home board completely with a 6-prime, which makes re-entry from the bar impossible. Even if the board isn’t closed, the fewer open points there are, the harder it is to re-enter.

As per the table above. If there are 3 open points you have a 75% chance of escape with one checker or 25% of escaping two checkers. If there is only 1 open point, the situation gets worse, with a 31% chance of escaping one checker and only a 3% chance of escaping two. For example, if we imagine that the one point is open. We can see that 11 rolls include a 1, which will allow one checker to escape. However, there is only one roll that includes two 1s that will allow both checkers to re-enter.

The average roll of two six-sided dice is 7. This would mean each turn would typically involve advancing a checker or checkers an average of 7 pips. However, because of the additional rolls added for a double, the actual average roll of two dice is 8.17. This means that every turn that you spend trapped on the bar will lose you an average of 8.17 pips in the race. It only takes a handful of missed turns for this to become a significant disadvantage. Consider for a moment the scenario above. Only the 1-point is open and we have one checker on the bar. There is a 31% chance of any roll escaping from the bar. This means it will typically take 4 rolls to re-enter the checker. In this time your opponent will have advanced 32 pips on average, giving them a considerable advantage in the race.

Related content

Backgammon Galore – FAQ