Last updated on May 21, 2024
The Deluxe Backgammon team took a high-level view of probability in one of our earlier posts. We presented a table that gave the preferred opening moves and the basic probability of rolling specific numbers or combinations. In this article, we will take a closer look at the theory behind those numbers. The understanding of probability will give you the knowledge to make calculated risks during play and ultimately improve your standard of play. If you are a novice and are ready to take your enjoyment of your luxury backgammon set even further, please read on.
Six-sided dice
Backgammon is a game of strategy and luck that is played with two standard six-sided dice. Each side of the dice has a number from 1 to 6. Opposing sides of the dice will always add up to a total of seven. During a turn in backgammon, it is the values rolled on the two dice that determine how a player can move their checkers around the board.
The numbers rolled can be split between two checkers or they can be totalled and used to move a single checker. For example, if a 3 and a 4 are rolled, the player has two options. They can move one checker three spaces and another checker four spaces, or one checker can be moved a total of seven spaces, assuming no points are blocked. There are movement restrictions based on whether or not points are unoccupied. (You can land on any point as long as it is not occupied by two or more of your opponent’s checkers).
Doubles
A roll of a double (for instance, two 4’s) needs to be considered separately because a double confers a bonus of two extra moves. A roll of two 4’s means that the player has four 4’s to use and may move any combination of checkers to achieve this requirement. Doubles also add to the mean roll of the two dice. Excluding the backgammon doubling effect, the average roll of two six-sided dice will always total 7. This would mean each turn would typically involve advancing a checker or checkers an average of 7 pips. However, because of the additional rolls awarded to a double, the actual mean roll of two dice in backgammon is raised to a total of 8.1667. This is where the backgammon rule of 8 comes into play.
Calculating probability
For a single die that has not been tampered with, each side has an equal chance of landing face up. There is a total of six possible outcomes, corresponding to each of the numbers from 1 to 6 on the die. Therefore, each number has a 1 in 6 probability of occurring on any particular roll. When rolling two dice we need to consider each die separately.
When we roll two dice, each die roll is completely independent of the other. If we consider all of the possible combinations of numbers that could be rolled by two dice, we come to a total number of 36 equally likely outcomes (6 x 6). Therefore, 36 is the denominator for all of our probabilities for a roll using two dice. The probability for any specific dice roll (for instance 1 and 2) is in 1/36.
Rolling a specific single number
The probability of rolling two dice and getting at least one specific number from 1 to 6 is relatively straightforward to calculate. For example, let’s say we need to determine the probability of rolling at least one 2 with two dice. In this instance, we need to know how many of the 36 possible outcomes include at least one 2. The possible rolls which satisfy this example are:
(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (2, 1), (2, 3), (2, 4), (2, 5), (2, 6)
- Five ways to roll one of that number on the first die.
- Five ways to roll one of that number on the second die.
- One way to roll that number on both dice.
This demonstrates that there are 11 ways to roll at least one 2 with two dice. Therefore, the probability of rolling at least one 2 with two dice is 11 in 36. This is useful to know. At first, glance, if you have a checker on the bar and the only safe landing place is the two-point, the situation will look dire. However, the above example still shows that you are likely to re-enter 31% of the time. That doesn’t look so bad.
Rolling a specific total
Any number from two to 12 can be obtained as the sum of two dice. The total can increase beyond this when you consider doubles. The probabilities for two dice totalling a specific sum are slightly more difficult to calculate as there are different ways to reach these totals. For example, there are three ways to roll a sum of four (1, 3), (2, 2), (3, 1). However, there are only two ways to roll a sum of 11 (5, 6), (6, 5).
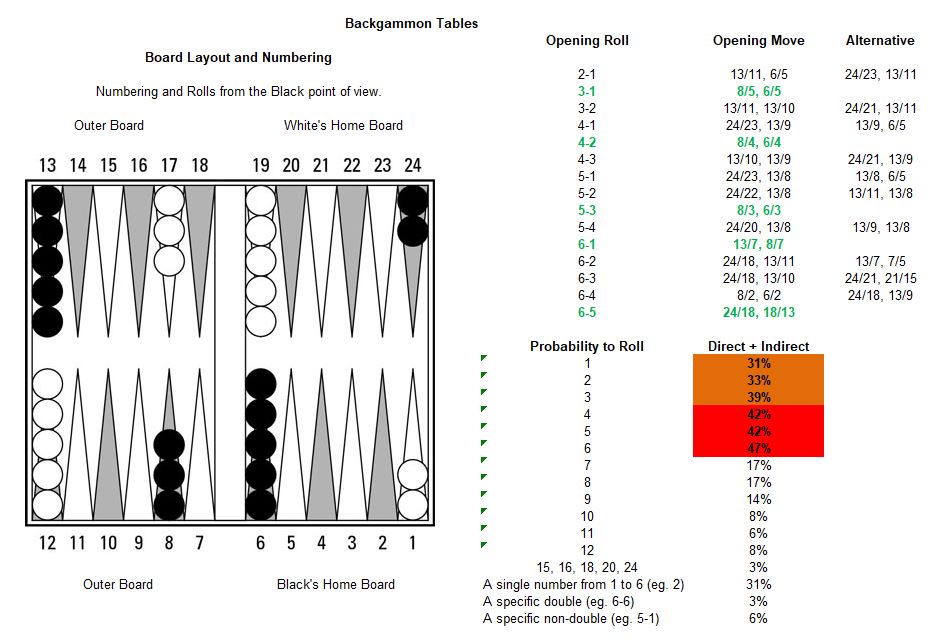
The screenshot above shows the probability to roll a specific number (direct and indirect). Direct is from the roll of a single die (1-6). Indirect requires the sum of both dice. The table assumes that the board is open for every possible throw. If part of the throw is blocked by an intervening point being held by opposing checkers, the chance of being hit is less.
Backgammon probabilities
This should cover the basics for calculating probabilities for backgammon. Rolling at least one of a number is mutually exclusive from rolling this number as a sum of two dice. We can therefore use addition to add the probabilities together for obtaining any number from 2 to 6.
For example, the probability of rolling at least one 6 out of two dice is 11 in 36. Rolling a 6 as a sum of two dice is 6 in 36 (including double 2’s & 3’s). The probability of rolling at least one 6 or rolling a six as a sum of two dice is 11 in 36 + 6 in 36 = 17 in 36 (47%). Other probabilities can be calculated in a similar manner.
Conclusion
If you need more detailed information there is much more information on the internet. If you can grasp the basics of probability it will enable you to make better strategic and tactical decisions during play. This is bound to help you enjoy the game even more. A complete list of Playing Guides is available on this link.
Related content
Here is a great page on probability from Pauls Pages.



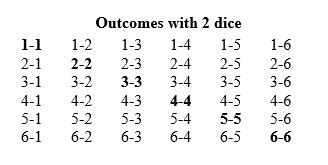
For example, there are three ways to roll a sum of four (1, 3), (2, 2), (3, 1).
What about 1-1?
Hi Metttyu, yes a 1-1 is a double and counts as four moves of 1. So it is another way of rolling a total of 4. Thanks for commenting, Jason